Număr vizualizări 3052 ori
Într-o zi, cred că era prin anii 1980, mă plimbam prin apropierea Porții Damascului. Chiar vizavi se află autogara Ierusalimului de Est, de unde pleacă autobuzele spre Ramallah, Hebron, Betleem etc. Deodată privirea mi s-a oprit pe ceva ciudat: toate inscripțiile de pe autobuze erau în arabă și chiar numărul liniei era ininteligibil. (Menționez că a fost cu ani în urmă – în zilele noastre se folosesc numerele obișnuite, dar în alte țări, de exemplu în Egipt, continuă să fie folosite cifrele arabe.)
Cifre arabe? Cum adică? Eu credeam că toată lumea folosește cifre arabe și doar în situații speciale se folosesc cifrele romane (clasa a III-a, Ludovic al XIV-lea, secolul XX…). Pe atunci nu era internet, așa că întrebarea a rămas fără răspuns. Poate a venit timpul să caut explicația? Cu aceeași ocazie ar trebui să văd și cum funcționează cifrele ebraice tradiționale, pe care niciodată nu le-am înțeles ca lumea.
Încă din zorii civilizației a apărut nevoia de a ține socoteala turmelor, a recoltelor, a birurilor, a datoriilor – o societate nu putea funcționa fără aritmetică. Cea mai veche formă de a ține socoteli erau crestăturile pe răboj. Acest obicei datează încă din epoca pietrei și în unele locuri s-a păstrat până la mijlocul secolului al XIX-lea!
În foarte multe culturi cifra 1 se scrie ca o linie și probabil la origine era o crestătură pe răboj. Dar în Europa medievală funcționa un sistem foarte sofisticat, unde se puteau scrie cu precizie numere mari: o crestătură de un lat de palmă era o mie, o crestătură cât degetul mare era 100, etc. iar cel care „citea” răbojul își folosea propria mână ca etalon.
În Orientul Antic, scrierea numerelor a apărut odată cu scrierea însuși, în urmă cu cca. 5000 de ani. În general cifrele nu aveau semne speciale, ci hieroglife, semne cuneiforme sau litere. Fiecare cultură și-a creat propriul sistem, au existat nenumărate variații, dar în Egipt / Grecia / Roma funcționau două sisteme de bază: sistemul hieroglific și sistemul alfabetic.
Era un sistem cât se poate de simplu, format din numai șapte semne, și totuși era genial, pentru că permitea efectuarea relativ simplă a operațiilor aritmetice de bază. Iată cum s-ar face o adunare, de exemplu 27 + 3 = 30
Ո Ո I I I I I I I + I I I = Ո Ո I I I I I I I I I I = Ո Ո Ո
Douăzeci și șapte + trei = „douăzeci și zece” = treizeci.
Principalul dezavantaj era că trebuiau numărate șiruri lungi de semne. Grecii au propus o variantă mai compactă, care avea semne și pentru 5, 50, 500 etc. Iar cifrele romane au fost încă un pas în aceeași direcție. De exemplu 29 era scris:
Ո Ո I I I I I I I I I – la egipteni
Δ Δ Π I I I I – la greci și
X X I X – la romani
Dar oare cum socoteau romanii? Și nu încape nicio îndoială că socoteau, pentru că au lăsat în urmă realizări inginerești remarcabile. Adevărul este că toată lumea folosea abacul. Era o simplă scândură cu jgheaburi în care se puneau pietricele. (Pietricică este în latină calculus – iată de unde vine calculatorul!)
Folosirea abacului este surprinzător de simplă și poate fi înțeleasă dintr-un videoclip de patru minute:
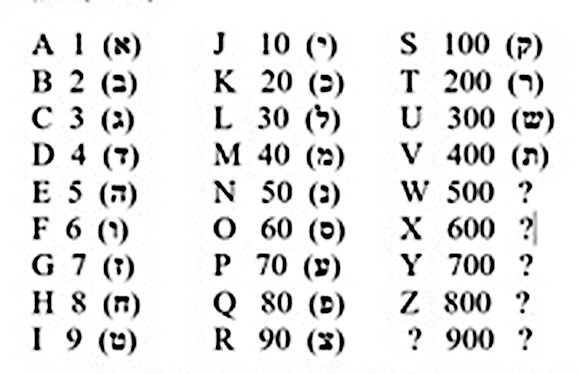
2. Sistemul alfabetic a apărut tot în Egipt, bazat pe scrierea „de mână”. (Hieroglifele erau folosite numai pentru inscripții săpate în piatră.) El a fost apoi perfecționat în coloniile grecești de pe coasta apuseană a Asiei Mici. În acest sistem, fiecare literă a alfabetului primește o valoare numerică. Dacă aș încerca să-l recreez cu alfabetul latin (sau cu cel ebraic), ar ieși cam așa:
În acest caz KD = 24 (כ”ד), SI =109 (ק”ט), VOI = 469 (תס”ט). Este un sistem foarte compact, dar are o serie întreagă de neajunsuri. Întâi de toate trebuia găsită o rezolvare pentru a scrie numere mai mari. Grecii aveau metode pentru a scrie numere foarte mari, fracții, operații aritmetice, inclusiv ridicarea la putere, exista un simbol pentru „o necunoscută” etc. Majoritatea tratatelor matematice păstrate din antichitate folosesc acest sistem. De exemplu, prin 250 î.e.n. Eratostene a calculat circumferința Pământului. Dar există foarte puține explicații despre felul cum se socotea.
Până în Evul Mediu timpuriu sistemul alfabetic s-a bucurat de un foarte mare succes, fiind preluat de diverse culturi și adaptat la diverse alfabete, printre care cel arab, ebraic, slavon, georgian, copt (Egipt), geez (Etiopia) etc.
Numerele ebraice. În viața de toate zilele în Israel se folosesc numerele obișnuite, folosirea numerelor ebraice se limitează la câteva cazuri speciale:
(‘א) Liste – ca cea de față,
(‘ב) Numerotare – clasa a V-a (ה’), la radio, programul III (ג’)
(‘ג) Numerotarea capitolelor și a versetelor din Biblie și din scrierile ebraice tradiționale.
(‘ד) Scrierea datei după calendarul evreiesc
(‘ה) Numerologie (ghematria), un sistem după care literele care alcătuiesc un cuvânt se înlocuiesc cu valorile lor numerice, acestea se însumează, iar rezultatul se presupune că are semnificații mistice (cel puțin pentru cei care cred în ele).
În folosirea numerelor ebraice apar câteva probleme:
*Cum deosebim un număr de un cuvânt? Un număr format dintr-o singură literă primește un apostrof (‘ב). Un număr format din mai multe litere primește ghilimele (תס”ט).
*Alfabetul e prea scurt, atunci cum scriem numerele mari? 500 se scrie ca 400+100 (ת”ק), 600 se scrie ca 400+200 (ת”ר) etc. Pentru mii se reiau de la început literele alfabetului, dar despărțite de restul numărului printr-un apostrof. De exemplu 3265 va fi (ג’רס”ה). În practică numerele mari se folosesc numai pentru a scrie anul de la facerea lumii. În cazul acesta miile se subînțeleg și anul curent, 5783, se scrie ca (תשפ”ג), adică 400+300+80+3 = (5)783. Pe internet se găsesc site-uri care transformă datele dintr-un sistem în celălalt.
*Unele grupuri de litere sunt evitate pentru că reprezintă o abreviere a numelui lui Dumnezeu. Astfel în loc de 15 se scrie 9+6 (ט”ו), iar în loc de 16 se scrie 9+7 (ט”ז)
Sistemul modern a fost inventat în India, dar a fost o dezvoltare treptată, e greu de spus când a apărut. În orice caz prin secolul al V-lea e.n. în India se folosea deja un sistem de nouă semne plus un punct sau un loc gol pentru zero, iar poziția fiecărui semn indica dacă sunt unități, zeci, sute etc. Semnele nu arătau ca cifrele de astăzi, dar logica folosirii lor era aceeași.
Arabii l-au cunoscut încă înainte de apariția islamului. Iată ce scrie învățatul creștin nestorian Severus Sebokht din Siria, în anul 662: Nu mai vorbesc de știința din India. … Descoperirile lor în astronomie le depășesc pe ale grecilor și ale babilonienilor, iar metodele lor de calcul sunt neîntrecute. Voi spune doar că aceste calcule se fac cu nouă semne… De la arabi, sistemul a ajuns în Europa, de unde și denumirea de „cifre arabe”, când de fapt ar fi fost mai corect „cifre indo-arabe”.
Popularizarea cifrelor arabe în Europa este de obicei atribuită italianului Fibonacci, în lucrarea Liber abaci (Cartea calculelor), scrisă în 1202. Dar acest sistem apare deja în Sefer hamispar (Cartea numerelor), scrisă de evreul spaniol Abraham Ibn Ezra pe la 1160.
Și ca să ne întoarcem la întrebarea de la care am pornit: cum se face că „cifrele arabe” aflate în uz curent în cea mai mare parte a lumii arată altfel ca cele folosite în țările arabe?
Timp de sute de ani cifrele au fost copiate cu mâna și forma lor s-a schimbat treptat, au apărut chiar două variante: una occidentală (în roz), folosită în Spania și Maroc, și una orientală în albastru), folosită în Orientul Mijlociu. Cifrele folosite în Europa au fost preluate de la cele occidentale. Forma standardizată a apărut numai odată cu folosirea tiparului. În Orientul Mijlociu, unele țări mai conservatoare continuă să folosească varianta orientală, altele au trecut treptat la folosirea cifrelor obișnuite.
* * *
Cititorilor curioși (și curajoși!) le propun o mică incursiune în cartea de matematică a lui Ibn Ezra, scrisă acum aproape 1000 de ani. O parte a textului se găsește pe Wikisource:
Interesant că ea a fost scrisă exact în perioada de trecere de la sistemul alfabetic la cel modern și le conține pe amândouă. Am încercat să buchisesc câteva fragmente.
Exemplu: 13×28 (י”ג על כ”ח).
Înmulțim 10×20=200 (‘י’ על כ’ = ר)
plus 10×8=80 (‘י’ על ח’ = פ),
la un loc sunt 280 (ר”פ).
Îl înmulțim pe 3 cu 20 (‘ג’ על כ) și apoi cu 8 (‘ח),
la un loc sunt 84 (פ”ד).
Totul împreună face 364 (שס”ד).
Înmulțirea este făcută în sistemul alfabetic. 13 X 28 este văzut ca (10+3) X (20+8), iar metoda lui este cea folosită la algebră: (a+b) (c+d) = ac + ad + bc + bd.
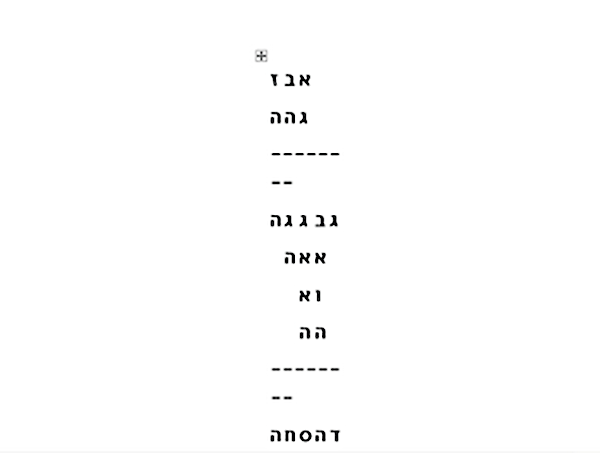
În schimb pentru înmulțirile cu numere mari, Ibn Ezra trece la sistemul modern:
Dacă ai de înmulțit două numere mari, va trebui să le scrii prin metoda celor 9 litere, așa cum ți-am arătat, și să le pui unul sub altul, așa încât literele să fie aranjate în coloane.
Numerele sunt transformate din sistemul alfabetic în cel modern. Ca „cifre” se folosesc primele nouă litere ale alfabetului ebraic și unde este cazul se pune zero. El dă ca exemplu 127 x 355 = 45085. (Sensul e „invers”, de la dreapta la stânga).
Metoda nu este exact cea pe care am învățat-o în școala primară, dar rezultatul e corect. Iar dacă cumva printre cititori se găsește cineva care știe ebraică mai bine ca mine, m-aș bucura să-mi explice și mie cum a procedat Ibn Ezra în exemplul de față – explicația se află în text, în link-ul de mai sus.
Hava Oren



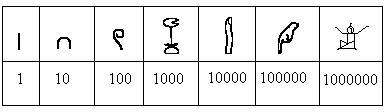




13 Comments
Teoria numerelor a rămas pănă astăzi unul din cele mai dificile si mai fascinante domenii ale matematicii, cu multe ipoteze, rezultate formulate prin intuitie, dar nedemonstrate, sau dovedite partial.
Probleme care isi asteapta rezolvatea de sute de ani, devenind celebre.
Dupa ce ati scris acest articol f interesant, s-a anuntat ca matematicieni au reusit sa demonstreze 2 astfel de Enunturi celebre. Afirmativ sau negativ, sau numai in anumite conditii speciale.
D-na Hava Oren, va felicit si pentru seriozitatea articolului dar si pentru intuitia fenomenala de a-l scrie tocmai acum.
Multumesc D-nei Hava Oren pentru articolul interesant si bine documentat .
Totusi fiindca subiectul este scrierea cifrelor vreau sa prezint o alta explicatie a formei cifrelor desi nu pot sa indic sursa.
Explicatia face legatura dintre forma in scris si continut ( adica valoarea numerica cantitativa a cifrelor ) si e inca o dovada de logica matematica..
Explicatia formei se bazeaza pe numarul de unghiuri la fiecare cifra :
– unu e reprezentat de doua laturi care formeaza un singur unghi
-doi e reprezentat de trei laturi care formeaza doua unghiuri ( seamana cu Z)
s.a.m.d. se adauga laturi si unghiuri
-zero nu are niciun unghi !
Pentru ca nu pot desena pe textul de fata propun
sa desenati cifra de opt ca doua triunghiuri varf in varf si sa numarati numarul unghiurilor interne si externe , opt in total .
Asta a fost initial : dar in scris probabil ca “varfurile ” s-au ” rotunjit ” si asa se face ca avem acum cifre moderne cursive mai usor de scris .( Si s-a uitat forma initiala )
Desi nu vin din lumea cifrelor nu pot sa nu recunosc ca matematica este limba cea mai universala .
” Cifre Arabe ” : se numesc asa pe drept considerand aportul important al matematicienilor arabi din Evul Mediu in
special la Algebra ( un cuvant arab ) .
Uraz sa traim in o lume in care intotdeauna
” doi si cu doi fac patru “! (cum spunea Orwell).
Foarte interesantă teorie și păcat că nu puteți indica sursa. Eu văd în ea părerea unui grafician. Mă întreb însă cum aplicați această teorie la alte sisteme de numerotare, ca de exemplu la cifrele romane sau ebraice. Dar chiar în cazul cifrelor obișnuite, ce faceți cu 6 și 9, care au același număr de „unghiuri și laturi”?
Fiindca sunt intrebari raspund:
Vreau sa mentionez ca este vorba de o explicatie si nu de o “Teorie “.
Cifrele romane sunt in parte cumulative , in scris, pe cand cele ebraice sunt arbitrare .
Cifra 6 are laturi necesare ca sa formeze sase unghiuri pe cand cifra 9 are mai multe laturi ca sa formeze noua unghiuri .
“Rotunjirea” unghiurilor a facut ca in scrisul modern sa fie identice ca forma si inverse.
Explicatia asta ( nu este a mea personala !) se bazeaza pe relatia dintre numarul de unghiuri si valoarea cantitativa a cifrei .
.Dupa mine e logica dar fiecare e indreptatit sa aibe parerea lui .
Un articol grozav,mi-a placut foarte mult,chiar am incercat sa rezolv cateva excercitii,totusi apartin si eu de lumea calculelor si a numerelor.Recunosc ca s-au miscat “rotitele”Multumesc ca le-ai pornit!
Am fost socata sa aflu ca cifrele arabe nu sunt de fapt arabe la origine, ci doar in cursul traseului lor spre vest au trecut si prin filera araba!! O traiectorie istorica a reprezentarii numerice prezentata in mod atractiv, informatiile se inlantuie in mod logic si mentin interesul cititorului de la primul cuvant pana la incheierea articolilui.
Complicat pentru unii dar interesanta istorie a numerelor.
Definitv pune logica la încercare, precum și un ascuțit simt al observarii detaliilor.
Multumim Eva!
Subiectul si continutul acestui articol mi-au starnit interesul sa-l recitesc de mai multe ori. Ca de obicei , articolul este bine documentat si ne ofera o perspectiva larga si probabil inedita in revista Baabel asupra ceea ce pentru majoritatea cititorilor ar fi parut banal. Felicitari pentru idea si profunzumea cu care ai abordat acest subiect.
Excelent articol!!! Am mai citit unele materiale asemănătoare, însă, niciunul nu a fost așa de complet ca acesta. Mulțumim mult pentru el !
Dragă Hava după cum te știu ai o răbdare de fier, ceeace dovedește și acest articol,
Pentru mine era necesară o viață să o scriu,
Felicitări !!
Un articol foarte interesant şi scris pentru profani, dar care totuşi trebuie citit de mai multe ori. Deşi matematica pare domeniul cel mai “universal”, după muzică, observăm cât de mult variază reprezentarea numerelor şi, mai ales, modul de a opera cu ele, de la popor la popor. Î
Articol foarte interesant si scris in mod inteligent care mi-a pus logica la treaba.
Asta era și intenția mea. La vârsta noastră nu strică să punem „rotițele” la treabă, ca să nu se atrofieze.